Numerical Simulations, Part 1 – Application of numerical simulations for investigation and improvement of the acoustic behaviour of vertically perforated bricks

Sound insulation of a single-leaf construction element

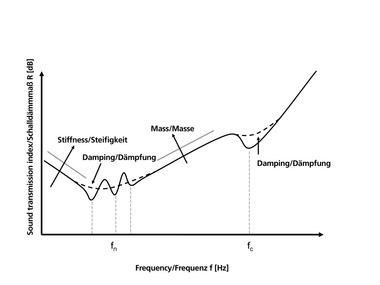
Besides the material parameters of vertically perforated bricks, their sound reduction index is also influenced by the configuration of the perforations in the vertically perforated bricks. In the past, diverse structure-borne sound measurements have been conducted on vertically perforated bricks by Gösele [1] and at the Fraunhofer Institute for Building Physics by Koch and Maysenhölder [2][3]. Here, besides the vibrations of the entire wall, individual brick vibrations in the form of flexural- and thickness-mode vibrations were determined. In the low and medium frequency range, the wall vibrates almost like a single-leaf and homogeneous element. From around 500 Hz both flexural- and thickness-mode vibrations of individual vertically perforated bricks are generated, leading to a reduction in the sound insulation in this frequency range. Thickness-mode vibrations can be observed in both homogeneous and inhomogeneous construction elements. However, the thickness-mode vibrations in homogenous building elements, in contrast to those in inhomogeneous elements, like walls made of vertically perforated bricks, occur above the building-acoustic-relevant frequency range and are therefore not taken into consideration in the sound reduction index. The frequency range in which the change in the frequency-dependent sound insulation takes place and the extent of this change are influenced by the configuration of the perforations, the size of the brick and the material properties of the body. In this connection, bricks with large perforations or cells show a strongly pronounced decline in the curve for the frequency-dependent sound reduction index. In contrast, in the brick with small perforations, no strong pronounced decline in the sound reduction index can be determined. Nevertheless, from around 500 Hz, the sound reduction index rises, not as expected according to Berger’s mass law by 6dB/octave, but shows a much flatter curve between 500 Hz and 1 000 Hz.

Description of the numerical simulation model for calculation of the sound transmission through walls built of vertically perforated bricks

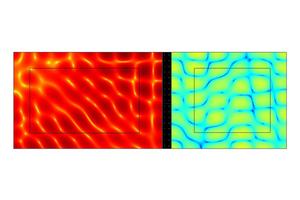
As part of an AIF research project conducted at the Brick and Tile Research Institute, a numerical simulation model was developed for calculation of the sound transmission through walls built of vertically perforated bricks. The simulation model was created based on DIN EN ISO 10140, which regulates the measurement of airborne sound insulation of construction elements in a test stand. Accordingly, sound reduction indices of walls built of vertically perforated bricks measured in a test stand can be qualitatively compared with the sound reduction indices numerically calculated in the simulation model. However, no agreements with an accuracy of 1 – 2 dB can be expected. First, as in tests performed by Meier [4] and also in the latest studies by Flieger et al. [5] in cooperation with the Physikalisch-Technischen Bundesanstalt PTB (Germany’s National Metrology Institute) in Braunschweig, within an interlaboratory survey, wide differences in the sound reduction index of a referent construction element measured in twelve different test stands were observed. Fig. »1 shows the results submitted by all participants as part of the interlaboratory survey.

As a result, depending on the test stand, the measurement results for the sound reduction index of a wall built with one and the same vertically perforated brick can differ widely. Moreover, with numerical calculations, simplifications of the model must be accepted, which will accordingly lead to deviations. On account of the high number of nodes that would be necessary for a three-dimensional approach in the frequency range from 100 Hz to 3 150 Hz, the numerical simulation model developed in this research project is reproduced two-dimensionally in a horizontal section. For this reason, in a comparison between numerically calculated sound reduction indices of walls built of vertically perforated bricks and those measured in test stands, no agreement with an accuracy of 1 – 2 dB is expected. Consequently, the goal is that the numerical simulation model reproduces the characteristic curve of a frequency-dependent sound reduction index of a vertically perforated brick wall and the decline in the sound reduction that results from individual brick vibrations and reacts correctly to changes in the respective input parameters. The numerical simulation model is therefore to be used for parameter studies and for optimization of vertically perforated bricks, and it will therefore contribute to a considerable reduction in time and costs. The numerical simulation model is thus not designed to serve as a substitute for final measurements of the sound reduction index in test stands, but as investigation tool even before fabrication of a prototype in the development process.

The development of the numerical simulation model for the determination of sound reduction of vertically perforated brick walls was based on DIN EN IS O10140-2:2010 [6], in which the measurement of the sound reduction of construction elements in test stands is anchored. Here, similar to test measurement, a source and a receiver room as well as a partition wall are modelled two-dimensionally. The two-dimensional simulation model is to reproduce a horizontal section of the test stands. The measurement of the sound reduction index in test stands is performed in accordance with DIN EN ISO 10140-2:2010 in third-octave bands in the construction-acoustic-relevant range from 100 Hz to 3 150 Hz. Here, the sound reduction index R results, as shown in the following equation, from the difference of the measured and then energetically averaged sound pressure level in the source room L₁ and receiver room L₂. In addition, a correction term, which results from the equivalent sound absorption area A in the source room and the area S of the test building element, is taken into consideration:

R = L₁ – L₂ + 10 lg

The numerical simulation model is shown in Fig. »2. In the source room (left in the figure), a diffuse sound field is generated and based on defined measurement areas the mean sound pressure level L₁ (source room) and the L₂ (receiver room ) are determine. From the difference between L₁ and L₂, the sound reduction index R is calculated over the frequency range in question. On account of the two-dimensional approach within the simulation, the correction term at the end of Equation 1 is not taken into account in the calculations. The airborne sound fields of the source and receiver room and the structure of the wall are discretized with an element size sufficient for the frequency range under consideration.

For a numerical simulation of the sound transmission through a wall built of vertically perforated bricks, besides an accurate drawing of the brick geometry, measurement of the brick body density and the dynamic modulus of elasticity is necessary.

Comparison of the results of the numerically determined sound reduction indices of walls built of vertically perforated bricks and those measured in the test stand

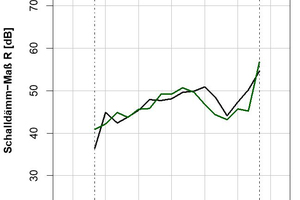
In the following, the results of the numerical simulation of the frequency-dependent sound reduction index of walls of large-perforation bricks of different thickness are presented and compared with real sound reduction indices from test stand measurements. Fig. »3 shows a numerical simulation of a vertically perforated brick with large perforations and a thickness of 365 mm. For this simulation, an already conducted test stand measurement was used. For this reason, it cannot be assumed that the material parameters of the vertically perforated brick, which were measured in the Brick and Tile Research Institute, agree exactly with the material parameters of the brick from the test stand measurement. Nevertheless, the numerical sound reduction index of the large-perforation brick in Fig. »3 shows very good agreement in both the high and the low frequency range.

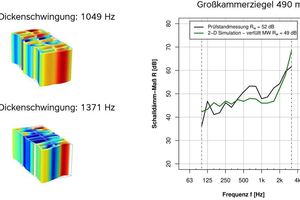
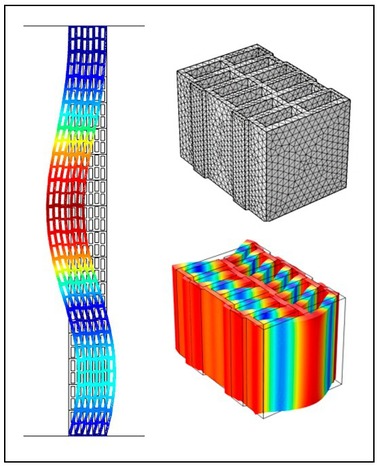
If we look at the numerically and empirically determined eigenfrequencies and eigenvibrations, which are shown in Fig. »4, then we can also easily recognize these in the curve for the sound reduction index in Fig. »3 in the frequency range between 1k Hz and 2k Hz as a decline in the curve.

As described in the second paragraph, individual brick vibrations, especially thickness-mode vibrations lead to a steep decline in the sound insulation of the wall. Both in the measurement and in the numerical calculation, the first thickness-mode vibrations were determined at around 1 300 Hz and 1 600 Hz and agree very well with the decline in the curve for the sound reduction index in Fig. »3.

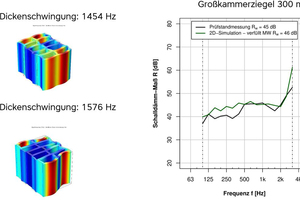
Fig. »5 shows the numerically calculated sound reduction index and that measured in a test stand for a large-perforation brick with a thickness of 300 mm. Moreover, the first thickness-mode vibrations of the vertically perforated brick are shown, which were determined numerically. Here, too, the numerical sound reduction index shows very good agreement with the sound reduction index measured in the test stand. The simulation model also effectively reproduces the sound reduction index of the wall built with these vertically perforated bricks.

Comparable results could be obtained for large-perforation bricks with a thickness of 490 cm. Fig. »6 shows a numerically calculated sound reduction index and one measured in a test stand for a large-perforation brick. In this study, the sound reduction index of the test stand measurement and the sound reduction index determined with a numerical simulation also show satisfactory agreement.

Summarizing, within the framework of these studies, it can be noted that the sound reduction index of large-perforation bricks of different thicknesses can be satisfactorily reproduced with the help of the numerical simulation model. Of course, occasionally, differences are determined between the numerically calculated sound reduction index and that measured in the test stand. First, a two-dimensional simulation model can reproduce the sound fields of a real room and the vibrations of a wall, however, the frequency-dependent curve of the sound reduction index of the numerical simulation agrees qualitatively with that from the test stand measurement. In addition, the two-dimensional numerical model satisfactorily reproduces the decline that results from the individual brick vibrations.

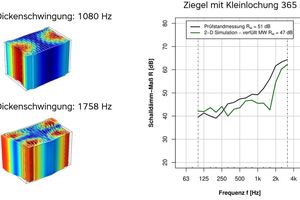
In addition, numerical calculations of the sound reduction index of vertically perforated bricks with small perforations were conducted and compared with test stand measurements. Fig. »7 shows the numerically determined sound reduction index and the sound reduction index from a test stand measurement for a brick with small perforations and a thickness of 365 mm. Here, too, the numerical sound reduction index shows good agreement with the test stand measurement. However, it can be noted that the numerical sound reduction index shows deviations of 10 dB at around 1 800 Hz. In this frequency range, as shown left in Fig.»7, a thickness-mode vibration occurs. In the numerical model, this vibration seems to have a stronger effect on the sound reduction index than is the case in reality. In this case, it must also be noted that this vertically perforated brick is filled for reasons related to thermal insulation. This filling of the vertically perforated is only considered in simplified form in the numerical model. Irrespective of this, the frequency-dependent sound reduction index of the wall built with these bricks can be well reproduced qualitatively with the help of the numerical simulation model.

Application of numerical simulations for the development of new vertically perforated bricks

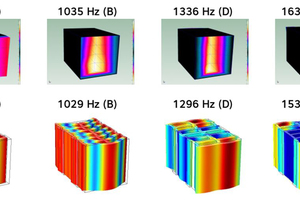
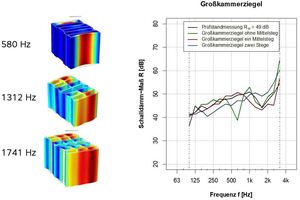
Following successful validation of the numerical simulation model for determination of the sound reduction index of vertically perforated bricks, here some examples of the application of the numerical simulations are shown. For example with the help of the numerical simulation model, the effect of a change in the configuration of a large-perforation brick on the sound reduction index can be investigated. Fig. »8 shows numerically determined sound reduction indices of large-perforation bricks without any internal web elements, with one internal web elements, and with two internal web elements. In addition, in Fig. »8, numerically determined single brick vibrations (first occurring thickness-mode vibrations) of the respective brick geometry are shown. For the brick without internal web elements, the first thickness-mode vibration occurs already at 580 Hz. This is reflected in the numerically determined sound reduction index at around 600 Hz as a strong decline in sound insulation. For the brick with one internal web element, the first thickness-mode vibration occurs at around 1 312 Hz. This can also be observed in the curve for the numerically determined sound reduction. For the brick with two internal web elements, the first thickness-mode vibration occurs does not occur until around 1 700 Hz. This leads to the sound reduction index of the wall built with this brick being considerably better in comparison with that for the brick with one central web element. In the medium frequency ranges the sound reduction index of the brick with two internal web elements lies at around 1 – 3 dB below the sound reduction index with one central web element. However, in the sound reduction index of the brick with two central web elements, hardly any decline in the sound insulation takes place and that leads directly to a better sound reduction index in the entire frequency range examined.

The selected brick perforations in this example do not, of course, correspond to the real configurations, however, this example is intended to show that the two-dimensional numerical simulation model effectively simulates the change in the brick configurations and can be used for the development of new vertically perforated bricks. Besides the geometry of the vertically perforated bricks, the effect of different material parameters on the frequency-dependent sound reduction index can be investigated.

Summary

Nowadays, numerical simulations are state of the art in research and development. Accordingly, at the Brick and Tile Research Institute, a two-dimensional numerical simulation model was developed for calculation of the sound transmission through walls built of vertically perforated bricks. It could be shown that the numerical simulation model can be used to satisfactorily determine the frequency-dependent sound reduction index both of walls built with bricks with large and small perforations. In addition, it could be shown that the numerical simulation model simulates individual brick vibrations and their influence on the frequency-dependent sound reduction index with acceptable accuracy. This numerical simulation model can be used for parameter studies and as a tool to support new development of vertically perforated bricks.