Material-specific moisture determination during brick drying

1 Introduction

The objective of drying green bricks is to remove any water necessary for plastic shaping prior to ceramic firing. For this purpose, convection drying is used. Control of the dryer in this process is generally empirically based. It is necessary to know the distribution of moisture and accordingly the drying progress in the green product. The local and time moisture gradient in the green product can be currently calculated in theory. However, depending on the position of the green brick in the dryer, the respective drying states and the moisture distribution over the cross-section normally differ. Accordingly, the local moisture and shrinkage gradients and therefore the risk of cracking are unknown. Core moistures can only be determined at the end of the drying process by means of destructive testing. To ensure the moisture content is below the maximum moisture values permissible for firing, drying is often performed longer than necessary. Current drying operation based on empirical values leads to ineffective drying process control. Shorter drying times and pinpoint drying can be achieved if the actual target value, the moisture content of the green product and especially the core moisture, is measured at every point in time during the drying process and is therefore known. Then a calculation programme into which the climate data and the material parameters of the green product are input can be used to calculate the drying progress and regulate it based on the measured moisture value.

2 Dielectric measurement methods

To determine the moisture value in the drying process, of the many measurement methods available, only dielectric methods can be considered. These can measure in a non-destructive, selective and accurate process. For determination of the moisture content, all dielectric measurement processes use the distinct difference in the dielectric material properties of water compared to that of the solid-state matrix. The complex-value permittivity ε of free water is many times higher than that of dry soil constituents such as loam or clay [8]. For this reason, a small variation in the water content leads to a considerable change in the permittivity of the sample overall.

For the determination of the moisture distribution in the green brick during drying, a measurement method is required that enables spatially resolved moisture measurement and determination of the core moisture. Such methods are based on principles with a transit time evaluation of a transmitted signal, like, for example, radar or TDR (time domain reflectometry). Both the reflection and transmission properties of the returned signal can be evaluated.

On the market, radar measurement systems are offered in various ways, however, commercial measurement equipment on the basis of dielectric methods for high-resolution determination of moisture distribution are currently not available.

2.1 Determination of the permittivity of brick clays in a wide frequency band

Crucial for the development of a dielectric measurement device is in which frequency ranges the system should function. The suitable frequency range depends essentially on the dielectric material properties, that is the permittivity. Cross-dependences with water content, density and temperature always exist [1, 4, 5, 7]. For example, in the relatively low frequency range (< 1 MHz), conductivity has a considerable effect on the resulting permittivity, which many measurement devices use as a measurement effect. In a higher frequency range (> 1 GHz) the penetration depth in the material decreases owing to the increase in power loss. To decide on a suitable frequency range, the permittivities of green product bodies are needed in a wide frequency range. This enables, on one hand, a complete description of the correlations, and specifically definition of the operational frequency of the measurement system.

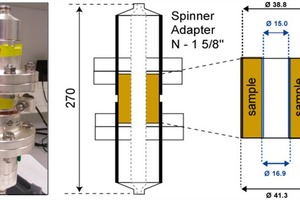
As a preferred process for the measurement of permittivity, a coaxial cell measurement was used. The measurement cell has an outer diameter of 41.3 mm, an inner diameter of 16.9 mm and a length of 50 mm (»1).

With two network analysers (NWA), the scattering parameters (S-parameters) were determined. The PNA E8363B network analyser from Agilent Technologies was used together with the “85071 Material Measurement Software E.3.01” (also from Agilent) to determine the permittivity in the frequency range from 100 MHz to 5 GHz. The ZVR-B25 network analyser from Rhode and Schwarz was used for the frequency range from 20 kHz to 200 MHz. Here, the permittivity was calculated with an inverse algorithm from the S-parameters, as specified in [2]. The measurement rig was set up similar to the set-up described in [2]. To compensate for systematic errors from the lead-ins and compounds, calibration was performed at the end of the cable with an electronic calibration module.

For a representative measurement result, the sample material must be installed undisturbed in the measurement cells, i.e. the material parameters such as density and moisture content should not change. For filling of the coaxial measurement cells, six working bodies and two clays were extruded in a cylinder shape. From these cylinders, the sample was cut out directly with a special tool into the measurement cells. The moisture content in the measurement was varied step by step from wet from the extruder to a completely dry state.

If the measurement results from all clays and working bodies are evaluated together, the frequency-dependent curve for the permittivity shows similar characteristics. For high volumetric water contents, the imaginary part increases considerably with falling frequency in the frequency range below 500 MHz. This increase becomes low when the volumetric water content falls below a certain value. In the real part, it is shown that the values in the low-frequency range fall with increasing frequency. If the volumetric water contents become very low, from 1 GHz, the value of the real part increases again. This described characteristic curve is shown in all clays and working bodies. As a result, the frequency dependence of the permittivity can be basically described with the same model.

2.2 Modelling of the permittivity of brick clays as a function of their water content

For modelling of the water-content- and frequency-dependent permittivity during drying, the green brick is regarded as a system of solid material (volume of clay and additive) and the capillaries. During drying accompanied with shrinkage, all capillaries are filled with water, at the same time the capillary volume decreases. As drying progresses, air penetrates into the capillaries so that the air volume must be taken into consideration. The resulting effective permittivity of the green bricks can be described with the extended Advanced Lichtenecker and Rother Model (ALRM).

⇥(1)

Where:

ρ stands for the porosity,

e_Db for the second relaxation process,

e_c describes the permittivity of the clay matrix and

e_W that of the water.

The factor Y_Db is equal to the volumetric water content Y when this is smaller than a limit water content Y_Dg. If the volumetric water content exceeds the limit value Y_Dg’ then the factor remains constant at the value Y_Dg. The second factor Y_fw is equal to the difference between the volumetric water content Y and the second limit value Y_fg in the case that Y lies above the second limit value of the water proportion and otherwise equal to zero.

That means the permittivity of the free water only has an influence on the resulting permittivity in very wet samples. With this extended blended model, the permittivity of the materials can be described completely as a function of the frequency, the volumetric water content and the density.

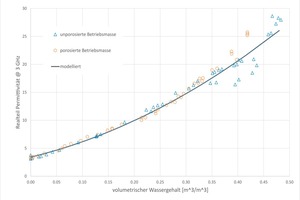
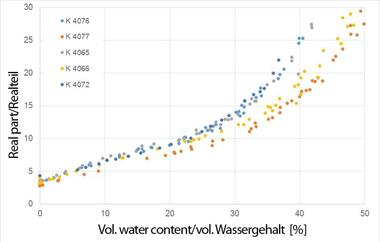
For the body without poreformer, the limit water content Y_Dg is 0.3 and for the body with poreformer 0.23. This leads to the influence of the second Debye process (in the range of the relaxation frequency, which lies in the MHz range) being input differently into the resulting permittivity. From this results that below around 1 GHz the values of body with poreformer differ from a body without poreformer.

In the frequency range above 2 GHz, the permittivity of a working body with a poreformer and working body without a poreformer from a brick plant exhibits the same dependence on the volumetric water content. In »2, the real part of the permittivity is shown at 3 GHz. Up to a volumetric water content of 0.35, the values are almost identical and can be adapted for this frequency with the same model. Accordingly, the additives do not change the resulting permittivity in this frequency range. From this results that the same dependences result – despite different mixing ratios for the production of the green brick body. Accordingly, a measurement system that functions at around 3 GHz can be used universally owing to the same dielectric properties of the different materials. With inversion of the correlations shown in »2, for the calculation of the volumetric water content Y, the following regression equation can be used:

100 · Y = 0.0011 · e_r³ – 0.114 · e_r ² + 4.35 · e_r – 13.3⇥(2)

This equation can be used in the programme for determination of the core moisture.

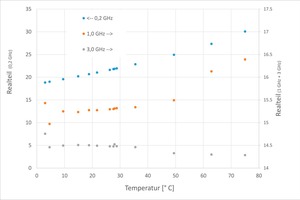
In addition, the above-mentioned cross-dependences must be taken into consideration, especially the dependence on the temperature as this varies widely in the dryer. If the temperature increases, especially the relaxation time is influenced, so that the real part of the permittivity decreases to a minimal extent in the GHz range (»2a). From this results that the temperature dependence of the permittivity at 3 GHz is negligible compared to the dependence on the water content.

Furthermore, the influence of the moisture gradients forming in the green brick on the resulting permittivity was studied. It is shown that the distribution of the water content in the drying green brick does not have an effect on the measured value for the total moisture. Accordingly, a dry green brick layer in the outer area that forms in the second drying stage does not influence the measurement.

3 Laboratory-scale concept for moisture measurement

For the locally resolved moisture measurement, a transit time analysis of a radar signal is taken into consideration. The velocity with which a signal passes through a green brick is slower than the speed of light by the root of the real part of the permittivity. With the inverse correlation

⇥(3)

and knowledge of the thickness d of the green brick from the transit time t, the real part e_r of the permittivity can be determined. The constant c corresponds to the speed of light in a vacuum. The real part of a wet green brick is around 25 at 3 GHz. From this, it results that the radar signal has passed through the green brick in just a few nanoseconds. So, a measurement system with a high time resolution is necessary. Suitable for the purpose is the ultra-wideband microwave radar system (UWB radar) m:explore from Ilmsens. The system is based on the M-sequence measurement method and has a transit time resolution of less than 100 ps. In this concrete case, it has a bandwidth of 0.1 to 6 GHz, so that a mean permittivity at 3 GHz can be used for calculation of the moisture content. Prototype patch antennas, which were developed by Ilmsens for m:explore, were used as antennas. The antennas are modified for direct connection to the measurement medium and to the mean permittivity. The measurements were conducted bi-statically, with a distance of around 5 cm between sender and receiver antenna.

With this measurement system, drying experiments to determine the moisture content were conducted in a time-controlled climate chamber. During these experiments, the air humidity as well as the air and surface temperature were measured as input parameters for the simulation of the experiment and the mass was measured (»3). For the measurement, the antennas were positioned in the close range to the measurement object (< 5 mm distance) to enable the best possible decoupling of the electromagnetic wave into the medium.

Owing to the chemically reactive substances in the green brick, the surface of the antenna became corroded during a coupling as shown in »3. For this reason, it was built into a shield casing and shielded at the rear to reduce reflections from the test set-up. To determine the exact point in time when the electromagnetic wave leaves the sender, reference measurements were conducted in reflection. For the ultrawide-band radar system and the designed antennas, an asymmetrical (unbalanced) connection was defined. The radar measurement system was therefore ready for operation for single-channel measurements. Depending on the moisture content, the bandwidth of the impulse reflected on the rear side of the brick. The pulse width of the reflected impulse lies below 1 ns. In the uncalibrated state, the system has a dynamic range higher than 40 dB.

The time curve of the temperature and relative humidity in the climate chamber were defined based on the drying processes in a drying chamber of a brick plant. However, the structural elements used do not allow any temperatures above 60° C, as a result of which only the process could be reproduced in principle. During the drying process, besides the climatic conditions, the mass and the impulse response of the UWB radar were recorded at a time interval of five minutes.

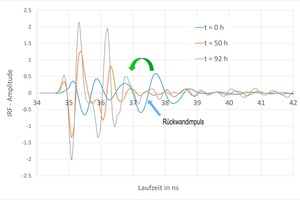
The signal of the impulse response (IRF amplitude) begins after around 35 ns to pass through the green brick and reaches after around 38 ns the rear side of the wet sample (»4). This characteristic impulse shifts as a result of the drying and the lower permittivity associated with it, which leads to low transit times, to an earlier point in time. With a Hilbert transformation, an enveloping curve can be calculated and accordingly the rear wall impulse can be described more clearly. With Equation (3), the transit time is evaluated, and the real part calculated.

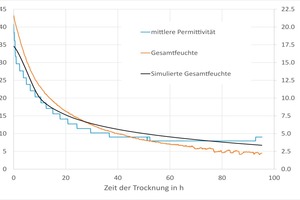
The time change of the permittivity can be compared with the curve of the measured and simulated total moisture »5. The simulation for this graphic was performed with DELPHIN. The material data necessary for this was previously determined and entered into the database. In the boundary conditions of the model in DELPHIN, the measured climate data were included.

»5 makes clear that the integral moisture and the water content can be measured over the entire drying process. The material properties dependent on the moisture content and density are taken into account. It does not matter how the moisture is distributed in the green brick. However, the measurement process does not enable the determination of the moisture distribution. For this, the core moisture is calculated.

4 Calculation of the core moisture

The material properties and of these especially the moisture conductivity as well as the drying conditions influence the moisture distribution in the green brick. With increasing coefficient of the moisture conductivity, the moisture gradients in the material decrease. This is also possible with low drying velocities. The core moisture can therefore be very different, at the same integral total moisture. The core moisture is defined as d/2±1/20, therefore a tenth of the green brick thickness around the centre of the green brick.

The climatic conditions in the dryer are defined based on the set drying curves in the brick plant. This offers the starting point for calculation of the time-dependent moisture distribution in the green brick. The numerical calculation of the transient moisture conduction is performed with the backwards difference process [6]. In this case, the determination of a so-called “water error” is used to check the achieved calculation accuracy. The backwards difference method enables the calculation of the first and second drying stage with consideration of the transient transport processes in the shrinking green brick described in [6]. From the material-specific, water-content-dependent permittivity, at any point in time during drying, the volumetric water content can be output. That means that based on the measured value of the permittivity and Equation (2), the associated water content is known. After transformation in a gravimetric water load, this is defined as the end water load. The calculation of the drying is performed up until the determined end water load.

The moisture and temperature distributions in dryers are often inhomogeneous. Therefore, the calculated drying time and the measurement time are compared. In the case of deviations, the chamber air condition on the rearward fog isotherm is adjusted until the deviation is minimal. This is done under the assumption that all green bricks have the same cooling air state. At the same time the air saturates during cooling as it flows over the green bricks so that green bricks facing away from the flow dry more slowly.

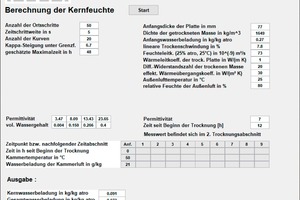
For this purpose, a programme was created with Matlab, which is suitable particularly for the calculation of the core moisture. The time- and position-dependent moisture content within the drying green brick is calculated with high resolution. So that the programme works as fast and effectively as possible, this is, however, not displayed graphically.

As the results, the core water load (d/10), the total water load and the total water content are output. »6 shows an image of the results of the core moisture calculation. On the user interface of the programme, the data in »6 top right describe the initial state of the green bricks including the green brick properties important for drying (hygrothermal properties) as well as the effective heat transfer coefficient prevailing on average in the chamber. The effective heat transfer coefficient consists of the convective heat transfer and the radiation. It also contains heat input in the green brick by the support surfaces [3]. Further in »6, left above the table, the water-content-dependent permittivity is described. These values must be entered for every material. If these are not known, prior to the actual measurement, a material function has to be created for use in calibration. On the right of this, the measured permittivity (real part) is input in the programme. From this, the volumetric water content is calculated.

Variable are the values in the cross-table. The drying is divided into a maximum of nine time sections, the starting time being entered into the second line. For these time steps, the chamber air temperature and the water load of the chamber air, and accordingly the drying programmes used in the plant are input. Thanks to the division into time steps, the green brick drying can be performed with a speed that is changeable over the time.

The example in »6 shows the drying of a vertically perforated brick with poreformer with average moisture conductivity. The green brick is dried at 50 °C and 26.5 % relative humidity for 12 hours. The measured permittivity results in a residual water content of 0.12 m³/m³. As the green brick is in the second drying stage by this time, the water content in the wet core is between the two drying levels. With knowledge of the momentary bulk density, from the water content the gravimetric water load is calculated. Further, the core water load (in this case 7.1 mm in the centre of the green brick) is calculated. In the concrete example, the surface is dry, the integral moisture value 7.3% bd, while in the core still 9.1% bd water is present.

5 Conclusion

The foundations have been laid for the determination of the core moisture of green bricks inside the dryer. The shrinkage and the large moisture measurement range with the associated changes in the moisture-content- and density-dependent material properties were taken into account. The developed, dielectric measurement method can capture the moisture content in the core, works non-destructively and quickly returns reproducible values. With the selection of the working frequency at 3 GHz, material and temperature changes have only a limited effect.

The measurement set-up could be successfully realized in the laboratory. At the same time, the boundary conditions for the transfer from laboratory into the dryer are shown. For the electronic components, structural elements are needed that withstand higher temperatures and a reactive environment. Another challenge is the incorporation of the calculation programme in the dryer control. This and the installation in the dryer are to be realized in another research project regarding the implementation of the measurement in the relevant equipment.

The AiF 18666 BG project of the Research Association of the Brick and Tile Industry was funded by AiF of Germany’s Federal Ministry for Economic Affairs and Energy pursuant to a resolution of the German Federal Parliament.