Measurement and numerical analyses of the acoustic
behaviour of individual vertically perforated bricks

1 Introduction

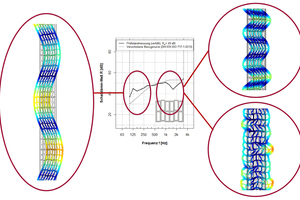
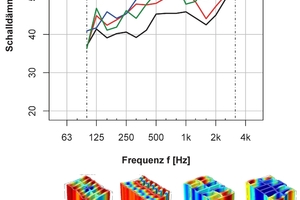
Like the density of vertically perforated bricks, the geometry of their perforations influences the sound reduction index of the entire wall. Structure-borne sound measurements have already been conducted by Gösele [1, 2] and the Fraunhofer Institute for Building Physics [3, 4, 5]; these determined the thickness-mode resonances and thickness-mode vibrations of individual vertically perforated bricks. In the case of thickness-mode vibrations, the opposite surfaces of the vertically perforated brick move out of phase, in contrast to bending-mode vibrations. »1 illustrates the frequency-dependent vibration behaviour of a wall built with vertically perforated bricks. In the low- to medium-frequency range to around 500 Hz, the wall vibrates almost like a single-leaf, homogeneous component. From around 500 Hz, both bending- and thickness-mode vibrations occur. In »1, thickness-mode vibrations with out-of-phase vibrating surfaces and bending-mode vibrations with in-phase vibrating surfaces can be seen.

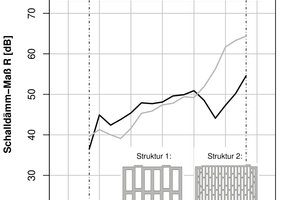
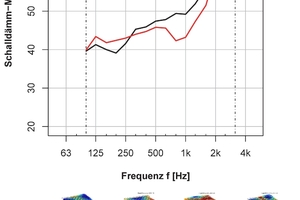
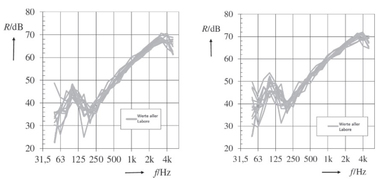
Thickness-mode vibrations occur both in homogeneous and in inhomogeneous components. However, in homogeneous components, in contrast to in inhomogeneous vertically perforated brick walls, the thickness-mode vibrations occur well above the frequency range relevant to building acoustics. Studies by Koch and Maysenhölder [3, 4, 5] show that in the case of thickness-mode vibrations, not the surfaces of the entire wall but rather the surfaces of the brick vibrate against each other. Here, much lower vibrations in the joints between the bricks can be observed compared to those in the middle of the brick surface, as can be seen in »1. Maysenhölder studied the vibration behaviour of perforated bricks with the help of experimental modal analysis and established the relation between the thickness- and bending-mode vibrations of the perforated bricks and the change in the sound reduction of the entire wall. In what frequency range the change in sound reduction takes place and the extent of this change are influenced by the geometry of the perforations, the size of the brick and the material properties of the brick body. In »2, two test set-up measurements of one vertically perforated brick with small perforations and one with large perforations are shown.

In this example, it can be seen how different the curve for the sound reduction of the two vertically perforated bricks is in the range between 500 and 2 000 Hz. The vertically perforated brick with large perforations shows compared to the vertically perforated brick with small perforations a different sound reduction at around 1 600 Hz. In the small-perforation brick, no pronounced change in the sound reduction can be determined. In contrast, from around 500 Hz, the sound reduction index does not increase as expected according to Berger’s law of mass by 6 dB/octave, but has a much flatter curve between 500 and 1000 Hz. These changes in sound reduction can be attributed to the thickness- and bending-mode vibrations of the individual vertically perforated bricks. Already from the curve of the sound reduction index, it can be observed that the individual brick vibrations differ from vertically perforated brick to vertically perforated brick.

2 Experimental and numerical modal analysis

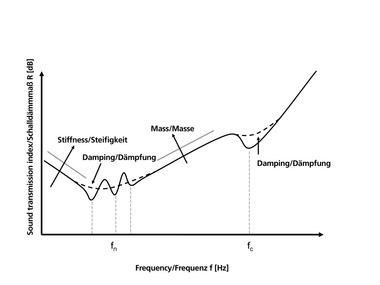
In acoustic measurement systems, modal analysis is a widely used method of testing for analysis of the dynamic behaviour of systems capable of vibrating when exposed to dynamic loads. With the help of modal analysis, the modal frequencies characteristic for a system with the associated mode shapes and modal dampings can be determined (also known as eigen frequencies, eigen vibrations as well as eigen dampings). If an excitation frequency agrees with an eigen frequency of a system, a resonant increase in amplitude results, from which, depending on the system, adverse effects, such as instabilities, failure or malfunctions can result. In the building acoustics discussed in this article, a resonant increase in amplitude leads to an increased sound transmission and therefore to an increased sound emission of a component. A modal analysis is defined only for linear models and does not provide information on the stresses actually occurring in the model as well as shifts under the applied loads.

Within the experimental modal analysis, the structure to be tested is excited at defined points. For this, for example, an impulse hammer (impulse excitation) or a shaker (signal excitation) is used. The resulting system responses (acceleration, speed or deflection) are again determined at defined measurement points. From the system excitations known in this way and the associated system responses, so-called frequency responses result, which describe the vibrating behaviour of the structure and from which the modal parameters can also be determined. Here the results are especially dependent on the prevailing boundary conditions. In addition, in the experimental modal analysis, the number and positioning of the measurement points (discretization) are important to obtain meaningful results. All defined measurement points of the structure to be tested must be accessible.

Besides the experimental modal analysis, eigen value analysis can also be analytically conducted for determination of the modal parameters (eigen frequency, eigen vibration, eigen dampening) of a system capable of vibration. To this end, the systems to be analysed are transferred into substitute systems consisting of masses, springs and dampers and their equations of motion in the form

⇥ (1)

formulated as a system of coupled differential equations. Here

M describes the mass matrix

D describes the damping matrix

K describes the stiffness matrix

describes the acceleration vector

describes the velocity vector

describes the displacement vector

describes the force vector of the system-exciting forces

If harmonic undampened vibrations are analysed, the system results as follows

⇥ (2)

With a solution approach for a harmonic vibration, an eigen value problem results, which after discretization and a numerical solution delivers the required eigen values. The term used here is linear modal analysis. With the help of numerical modal analysis, relatively large frequency ranges can be analysed in an uncomplicated way.

An advantage of numerical modal analysis is its possible application at a very early planning stage, long before any practical realization. Also with the application of numerical modal analysis, complex geometries as well as relatively large frequency ranges can be analysed fast and at low cost. As in the development of a model for a numerical modal analysis, always some simplifications and assumptions (incl. material properties and boundary conditions) must be made, parallel application of experimental and numerical modal analysis as well as a comparison of the results are expedient for the purpose of validation [6, 7, 8].

3 Comparison between experimental and numerical modal analysis

For the experimental and numerical tests, a vertically perforated brick with small perforations and one with large perforations, as shown in »2, were selected.

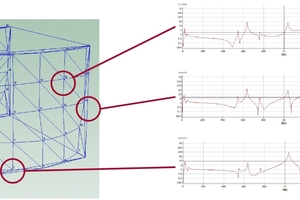
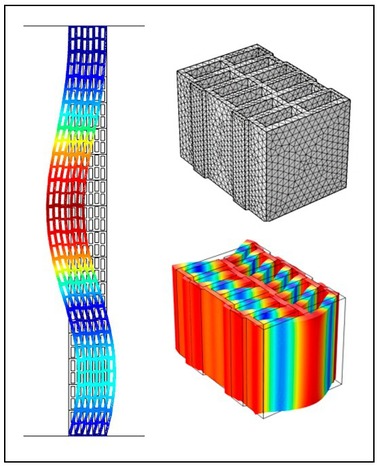
The front surfaces of the vertically perforated bricks were covered with a measurement grid, and this was excited with an impedance hammer. Moreover, an accelerometer was fixed to the front surface of the vertically perforated brick. In the tests of individual vertically perforated bricks, the bricks were positioned on bubble wrap to decouple the subsurface from the vertically perforated brick being measured. Here, it is important that on account of the mass-spring system formed, the resonance frequency lies as low as possible and outside the frequency range to be measured. After excitation of the vertically perforated bricks with the impedance hammer at the respective measurement points, the specific frequency response between excitation point and measurement point to which the accelerometer is fixed is obtained. In »3, the measured system responses with the experimental modal analysis are shown.

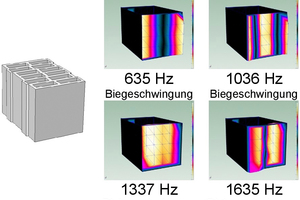
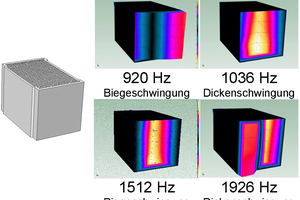
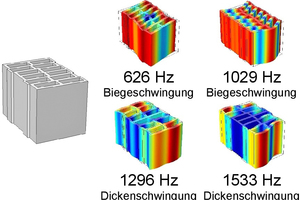
The sharp peaks indicate the previously described eigen vibrations. In this test it was necessary to test both front sides of the vertically perforated brick by means of modal analysis, so that the type of vibration can then be identified from the vertically perforated brick model in »3. In the case of in-phase vibration of the two surfaces, the eigen frequency can be attributed to a bending mode vibration and in the case of out-of-phase vibration to a thickness-mode vibration. »4 and »5 show the results of the experimental modal analysis for one vertically perforated brick with small perforations and one with large perforations.

Here in the large-perforation vertically perforated bricks, the individual brick vibrations occur already from 635 Hz, in the small-perforation vertically perforated bricks only from 920 Hz. If we look at the curves for the sound reduction index of the two vertically perforated bricks shown in »2, the curve of the small-perforation vertically perforated bricks does not show any substantial change in the curve for the sound reduction index. However, in the medium-frequency range, a much flatter curve for the sound reduction index can be seen. In contrast, for the large-perforation bricks, a considerable change in the curve for the sound reduction index can be seen, both at around 1 200 Hz and particularly at around 1 600 Hz. These changes in sound reduction agree with the thickness-mode vibrations at 1 337 Hz and at 1 635 Hz determined in the experimental modal analysis. Measurement with experimental modal analysis is an effective tool to test individual brick vibrations. The process, however, is time-consuming and can only be applied to already produced vertically perforated bricks. It is interesting to compare the results between the experimental and numerical modal analysis, especially in respect of further parameter studies and optimizations of the perforation geometries of vertically perforated bricks.

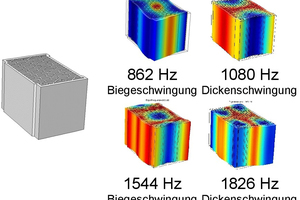
For the numerical modal analysis, the density, the dynamic modulus of elasticity and the Poisson’s ratio of the vertically perforated brick must be determined. Here the dynamic modulus of elasticity was determined based on the transmission of sound by means of ultrasound in the x, y and z directions. In »6 and »7 the numerically determined eigen frequencies with the associated mode shapes for the large- and small-perforation vertically perforated bricks are shown. The results for the numerically and experimentally determined eigen frequencies show good agreement. It cannot be expected that the numerical and experimental modal analysis agree exactly for every frequency. Both with the experimental and the numerical calculations, a scatter of results can be expected. Here different material parameters, boundary conditions or even individual small cracks in the body material can lead to measurement results deviating from each other. For this, the eigen frequencies and the respective mode shapes from the many individual frequency responses are combined to form one frequency response with the help of the superposition principle. This and many other factors lead to a scatter of results in this test. However, it is not actually necessary to determine the eigen frequencies so precisely.

4 Parameters study

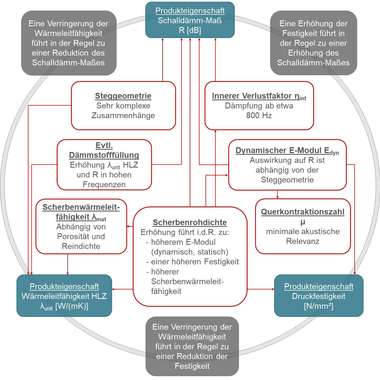
On the basis of the good agreement between experimentally and numerically determined eigen frequencies of the vertically perforated bricks tested, the numerical brick models were used for parameter studies. Tests were performed to ascertain which parameters have the greatest influence on the eigen vibrations of the vertically perforated bricks in order to derive possibilities for optimization of vertically perforated bricks.

4.1 Influence of the brick thickness on the eigen vibrations

As the first parameter, the influence of the thickness of the vertically perforated brick on the eigen vibrations and subsequently on the sound reduction of the entire wall was investigated. Theoretically, an improvement in the sound reduction of the entire wall can be expected with the use of a thicker brick on account of the additional mass per unit of area.

Tests (»8) show that the numerically determined eigen frequencies of the vertically perforated brick with a thickness of 42.5 cm turn out lower than those of the 36.5-cm-thick brick. This can also be observed in the measured sound reduction index of an entire wall built of vertically perforated bricks. It can be seen that the change in sound reduction is much more pronounced, shifting in the direction of the low frequencies. Although the mass per unit of area of the wall is increased because of the thicker vertically perforated bricks, this does not lead to an improvement of the measured sound reduction index of an entire wall.

Like the test from »8, the vertically perforated brick with large perforations (»9) shows an identical behaviour. However, in the curve for the sound reduction index, although the eigen frequencies of the vertically perforated bricks are decreasing, an improvement can be observed as a result of the increase in the mass per unit of area. An exception is the 49-cm-thick vertically perforated brick. Although this shows a higher mass, the sound reduction index lies below that of the 42.5-cm-thick vertically perforated brick. If the thickness modes vibrations of the vertically perforated bricks are compared with the slumps in the curve for the sound reduction index of the entire wall, these agree, as in the previous study, with the eigen frequencies.

4.2 Influence of the material parameters on the eigen vibrations

In the next step, the influence of the material parameters on the eigen vibrations of the vertically perforated brick with large perforations was tested.

»10 shows the numerically calculated eigen frequencies as a function of the different body density and the dynamic modulus of elasticity. Here it can be seen that the increase or decrease in the modulus of elasticity and the body density have no significant influence on the eigen frequencies of the vertically perforated brick.

4.3 Influence of the perforation geometry on the eigen vibrations

In contrast, the results in »11 with a change in the perforation geometry have a strong influence on the eigen frequencies of the vertically perforated brick.

In the test, a vertically perforated brick was modelled without as well as with one and two cross-webs and with diagonal webs. The eigen frequencies of the vertically perforated brick without cross-webs have, in comparison with the vertically perforated bricks with cross-webs, the lowest eigen frequencies. Here the surface of the vertically perforated bricks can vibrate completely freely and consequently impair sound reduction over the entire wall. With the addition of cross-webs, this vibrating behaviour is reduced, as a result the eigen frequencies are shifted to a higher frequency range. It can be seen that the vertically perforated brick with two webs shows much higher eigen frequencies compared to those of other tested models. Interesting is the test of the vertically perforated brick with diagonal webs. The crossing leads to the eigen frequencies of the bending mode vibrations increasing in comparison with those of the brick with one cross web and the eigen frequencies of the thickness-mode vibrations decreasing.

5 Summary and outlook

First the frequency-dependent vibration behaviour of a wall built of vertically perforated bricks was shown by way of example. Walls built with vertically perforated bricks vibrate in low-frequency range like homogeneous panels. From the medium-frequency range, individual vibrations of the vertically perforated bricks are shown, which are described as bending and thickness vibrations.

With a realistic modelling of the brick geometries and the properties of the body material, a good agreement of the determined modal parameters from the experimental and numerical modal analyses is shown. Building on this, a parameter study was conducted, to identify the most important influencing factors on individual brick vibrations of vertically perforated bricks with regard to further optimization of the brick geometries. Here, with a wall thickness that is too thick (> 42.5 cm), effects on the position of the individual brick vibrations result. In contrast, variations in the body density and the dynamic modulus of elasticity showed no significant effects on the individual brick vibrations.

The biggest influence was shown with changes of the brick geometries, which consisted, for instance, from the integration of additional cross and diagonal webs. With increasing stiffening in the transverse direction of the brick, the individual brick vibrations shift to higher frequency ranges. Accordingly, the brick geometry besides the material properties is the most important means of adjustment in view of optimization of the vertically perforated bricks.

For this reason, in following tests, other brick geometries are analysed in view of the vibrating behaviour of individual bricks. Here different vertically perforated brick types are selected, which represent steadily achieved improvements in sound reduction by the brick and tile industry based on further development of the web geometries.

So as the overarching objective, with the help of measurement and numerical modal analyses, attempts are to be made to further optimize the already high sound reduction indices of walls built with vertically perforated bricks. With further optimization in respect of the sound reduction index, walls built from vertically perforated bricks can find further applications in areas with increased requirements for sound insulation of external building components.

Institut für Ziegelforschung Essen e.V.
www.izf.de